Zamieszczona poniżej ciekawostka (w wersji angielskiej) była odrzucona przez: Nature, Science, Physics Reports, Reviews of Modern Physics, Physical Review Letters i arXiv bez wysłania do jakiegokolwiek recenzenta 🙂
Proszę o sugestie uzupełnienia tej listy.

Mimo, że mechanika kwantowa jest taka sama dla obiektów małych i dużych, istnieje przekonanie, że te ostatnie nie przejawiają typowo kwantowych zachowań jak superpozycja i interferencja. Historycznie taki punkt widzenia jest zawarty w tak zwanym paradoksie kota Schrödingera, gdzie zwierzę, zgodnie z prawami mechaniki kwantowej, jest przygotowane w superpozycji dwóch stanów: żywym i martwym. Paradoksalnym jest, że nikt nigdy nie widział, aby duży obiekt był jednocześnie żywy i martwy albo w dwóch różnych miejscach naraz.
Ten tekst ma za zadanie pokazać, że nie ma żadnej różnicy, z punktu widzenia mechaniki kwantowej, czy obiekt jest duży czy mały. Cechy kwantowe mogą być równie dobrze niewidoczne dla obiektów z mikroświata. Co więcej, przejście ze świata mikro do makro nie wymaga przekraczania żadnej kwantowo-klasycznej granicy, ani nie wymaga zewnętrznego środowiska do rozwiązania paradoksu.

Wstęp

Mechanika kwantowa (MK) jest rozwijana od ponad 80-ciu lat ale to nie jest teoria dojrzała. Przeciwnie, podstawowe jej kwestie są ciągle przedmiotem sporów. Jakie ma znaczenie funkcja falowa — czy opisuje ona jedynie zespoły statystyczne czy również pojedyncze obiekty? Jaki jest status procesu pomiaru — czy potrzebny jest do niego miernik klasyczny czy kwantowy? Czy pomiar jest częścią teorii kwantowej?
Nawet jeśli poprawne odpowiedzi na te pytania są już dostępne w literaturze, to na pewno nie ma jednomyślności wśród fizyków, które to.
W takim przypadku przykład, który w jasny sposób rozwiązuje jeden z istotnych problemów w MK może być ciekawy dla naukowców.
Poniżej, bez utraty ogólności rozumowania, będzie rozważana superpozycja przestrzenna dwóch stanów zamiast superpozycji żywy i martwy. Położenia jest znacznie łatwiej kwantyfikować niż wigor życiowy zwierzaka.
Słynny eksperyment Younga z dwoma szczelinami, który jest znakomitym narzędziem rozważań nad zawiłościami MK, pomoże w zilustrowaniu rozwiązania paradoksu kota Schrödingera.

„Paradoks” pojedynczego fotonu.

Dwie szczeliny umieszczone na drodze fotonów generują wzór na ekranie znajdującym się za nimi, Rys. 1. Każdy foton, który przeszedł przez szczeliny zostawia na tym ekranie jedną malutką plamkę. Wzajemne położenie szczelin i ekranu wpływa na kształt obrazu, który wyłania się po zarejestrowaniu wielu fotonów.

Rys. 1. Eksperyment Younga z ekranem blisko szczelin (t = 0.02) lub daleko od nich (t = 2.2).

W szczególności, jeśli ekran jest blisko szczelin to powstanie na nim obraz tych szczelin w postaci dwóch oddzielnych pionowych prążków.
Każdy żółty punkt na ekranie, Rys. 1., można powiązać z konkretną lewą lub prawą szczeliną, przez którą przeszedł foton, który ten ślad zostawił. Lewy prążek odpowiada lewej szczelinie a prawy prawej. Jeżeli ktoś zasłoni, powiedzmy, prawą szczelinę to, co prawda, prawy prążek zniknie ale lewy pozostanie taki sam.
Jeśli ekran jest daleko od szczelin to pojawią się na nim prążki interferencyjne. Nie można w takim przypadku dociec, którą szczelinę pokonał foton zostawiający konkretną plamkę na ekranie. Świadczy o tym sama obecność prążków interferencyjnych. Jakakolwiek udana próba ustalenia, którą szczeliną przyszedł foton zniszczyłaby prążki interferencyjne.
W obydwu przypadkach, ekran blisko szczelin lub daleko, kwantowy stan fotonu jest superpozycją dwóch możliwości: foton przeszedł przez lewą szczelinę i foton przeszedł przez prawą szczelinę. Ale w pierwszym przypadku, gdy ekran jest blisko szczelin można powiedzieć, którą szczeliną przeszedł foton, bo obydwa stany z superpozycji są rozseparowane przestrzennie, Rys. 2 a).

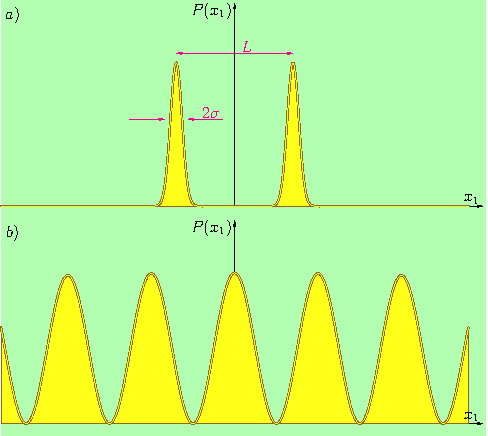
Rys. 2. Gęstość prawdopodobieństwa wzdłuż przerywanej linii na ekranie z Rys. 1 umieszczonym a) blisko szczelin (t = 0.02) lub b) daleko od szczelin (t = 2.2).

Jeśli ktoś sformułowałby „paradoks pojedynczego fotonu” w taki sposób: Dlaczego nie widać superpozycji fotonu w przypadku, gdy ekran jest blisko szczelin? Przecież jest on przygotowany w superpozycji stanów lewa-szczelina + prawa szczelina. to odpowiedź byłaby oczywista. Superpozycji tej nie widać, bo pojedynczy foton zostawia tylko jedną plamkę na ekranie albo w lewym albo w prawym prążku. Co prawda, mogłoby się zdarzyć, że plamka pojawiłaby się pomiędzy prążkami. W takim wypadku nie byłoby wiadomo, którą szczeliną przeszedł foton. Jest to jednak tym mniej prawdopodobne im większy jest iloraz L/σ. O superpozycji można byłoby mówić, gdyby powtórzyć eksperyment z jednym fotonem wielokrotnie i rejestrując całe prążki. Wówczas obecność prążków świadczyłaby o suprpozycji (lub o stanie mieszanym).
Zastępując słowo „superpozycja” słowem „interferencja” w sformułowaniu paradoksu pojedynczego fotonu można udzielić następującego wyjaśnienia. Dwa stany z superpozycji są przestrzennie rozdzielone i nie jest możliwa interferencja między nimi. Lewy prążek jest tworzony przez fotony przechodzące lewą szczeliną a prawy prawą.
W przypadku ekranu oddalonego od szczelin jeden foton tak samo nie wykaże superpozycji. Jeśli jednak eksperyment będzie powtórzony wielokrotnie to na ekranie pojawi się obraz interferencyjny, Rys.2 b). Aby to udowodnić wystarczy zasłonić jedną ze szczelin i prążki interferencyjne się nie pojawią.
Podsumowując, pojedynczy foton zachowuje się podobnie do hipotetycznego kota Schrödingera w przypadku, gdy ekran jest blisko szczelin. Mimo, że jest przygotowany w superpozycji stanów lewa-szczelina + prawa-szczelina nie wykazuje ani śladu superpozycji czy interferencji. Jeśli eksperyment jest powtarzany wiele razy jego wyniki wykażą fotony, które przeszły tylko lewą szczeliną lub tylko prawą szczeliną.
Podobnie każdy kot jest obserwowany tylko żywy lub tyko zdechły. To podobieństwo jest wykazane w następnej części.

Stan kota Schrödingera

Istnieje wiele równoważnych wersji paradoksu kota Schrödingera. Ich istota opiera się na superpozycji obiektów złożonych z ogromnej liczby mniejszych obiektów kwantowych.
Można taką superpozycję stworzyć w układzie Younga. Wyglądałaby ona tak: N fotonów przechodzi przez lewą szczelinę i żaden przez prawą plus żaden foton nie przechodzi przez lewą szczelinę i N fotonów przez prawą. N jest rzędu liczby Avogadro t.j. około 10²⁴.
Symbolicznie taki stan można zapisać jako:

(1)  

gdzie pierwsze miejsce w nawiasie |…, …〉 zajmuje liczba fotonów przechodzących przez lewą szczelinę, która będzie później reprezentowana przez krzywą Gaussa o środku w -L/2, a drugie miejsce przypada liczbie fotonów przechodzących przez prawą szczelinę reprezentowaną przez krzywą Gaussa o środku w L/2.
Stan z jednym fotonem, który był rozważany powyżej ma też taką formę ale z N = 1.
Prążki, ale nie pojedyncze plamki, pojawiające się na ekranie są całkowicie określone przez stan z Równania (1). Dla N = 1 gęstość prawdopodobieństwa wzdłuż przerywanych linii na ekranach z Rys. 1. ma taką postać:

(2)  

gdzie x₁ jest zmienną opisującą pozycję wzdłuż tej linii, L jest odległością szczelin, σ≪L odpowiada szerokości szczeliny a parametr t oznacza odległość ekranu od płaszczyzny szczelin. Równanie (2) ma ciekawą strukturę, jest sumą trzech komponentów. Dwa pierwsze to proste obrazy szczelin na ekranie, a trzeci to człon interferencyjny.
Jeśli odległość ekranu od szczelin jest mała t.j. t≪σ, to człon interferencyjny jest tłumiony przez eksponentę L²≫ σ² i tylko dwa obrazy szczelin pozostają, Rys. 2 a).
Z drugiej strony, dla ekranu odległego od szczelin t.j. t/σ≫L człon interferencyjny będzie dominujący, Rys.2 b).
W przypadku, gdy fotonów jest więcej niż jeden, obraz się nieco komplikuje. Każdy z fotonów dokłada nowy wymiar do gęstości prawdopodobieństwa. Dla N fotonów Równanie (2) zamienia się w:

(3)  

gdzie j numeruje fotony. Mimo wielowymiarowej postaci, gęstość prawdopodobieństwa ma taką samą strukturę jak w przypadku jednego fotonu: dwa pierwsze składniki odpowiadają obrazowi szczelin w N-wymiarowej przestrzeni rozpiętej przez położenia x₁, …, x_N, a trzeci człon jest składnikiem interferencyjnym.
Wielowymiarowa analiza Równania (3), nawet dla N ∼ 10²⁴, jest łatwa. Człon interferencyjny jest tłumiony jeszcze bardziej niż poprzednio z powodu czynnika N w eksponencie z L². Dwa pozostałe wielowymiarowe gaussiany mają szerokość daną promieniem √(σ² + (t/σ)²) i są umieszczone wokół punktów (x₁ = −L/2, …, x_N = −L/2) i (x₁ = L/2, …, x_N = L/2).
Geometryczna odległość środków tych gaussianów wynosi L√N, co jest dużą wielkością dla umiarkowanych odległości ekranu od szczelin t. Stąd te dwa składniki gęstości prawdopodobieństwa są przestrzennie rozdzielone z powodu dużej liczby fotonów budujących stan kota Schrödingera.
Innym sposobem analizy gęstości prawdopodobieństwa z Równania (3) jest użycie jednowymiarowego cięcia x/√N = x₁ = … = x_N wzdłuż linii przechodzącej przez środki wielowymiarowych gaussianów czyli przez dwa punkty (x₁ = −L/2, …, x_N = −L/2) i (x₁ = L/2, …, x_N = L/2)

(4)  

Cięcie pokazuje, że duża liczba N tłumi człon interferencyjny i oddala środki obydwu krzywych Gaussa o czynnik √N. Tutaj znowu dwie krzywe Gaussa (obrazy szczelin) będą przestrzennie rozseparowane dla umiarkowanych wartości t. To z kolei implikuje znikanie wzoru interferencyjnego nawet dla ekranu mocno oddalonego od szczelin.

Podsumowanie

Zmieniając N w Równaniach (2) i (3) od 1 do 10²⁴ można prześledzić przejście z mikro- do makroświata. Odległość przestrzenna dwóch wielowymiarowych krzywych Gaussa będących obrazami szczelin w gęstości prawdopodobieństwa wzrośnie z L do 10¹²L. Dlatego w przypadku makroskopowym eksperyment na pojedynczym kocie musi dać wynik albo kot przeszedł przez lewą szczelinę albo kot przeszedł przez prawą szczelinę.
Przejście z mikroświata do makroświata jest płynne i nie ma żadnej granicy pomiędzy jednym a drugim. W istocie zachowanie się kota Schrödingera jest bardzo podobne do pojedynczego fotonu w eksperymencie Younga, w którym ekran umieszczono blisko szczelin. Brak superpozycji i interferencji w obydwu przypadkach ma identyczne wyjaśnienie. Można powiedzieć, że stan kota Schrödingera jest równie tajemniczy jak stan pojedynczego fotonu.

Schrödinger’s cat versus photon (pdf)

Zbigniew Karkuszewski, 19 grudnia 2013