你是否曾经考虑过如何推导出著名的E=mc2公式?
这是否需要掌握相对论或更复杂的理论?
实际上,不需要!
所需的技能仅仅是一些高中物理知识和一点好奇心。
下面的图中有一个质量为 M 的盒子,水平长度为 L。在静止状态下,盒子的质心悬挂在 ×c 点上方的某处。
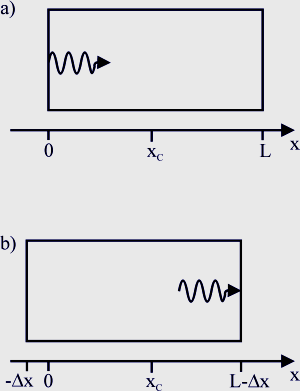
要推导这个公式,只需回答一个问题:如果从盒子的左墙发射一个光子(如图 a 所示),并在右墙被捕获(如图 b 所示),质心的位置会发生什么变化?
假设光子的能量为 E。已知光子以光速 c 传播,并携带动量¹。
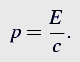
From the momentum conservation principle, after the photon emission, the box should move leftwards with some velocity v. After the photon is absorbed the box must stop due to the momentum conservation.
The velocity v is calculated in the following manner.The box moves the distance Δx to the left before the photon hits the right wall. Time of flight of the photon Δt is given by
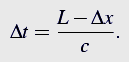
Thus, the mean velocity v of the box
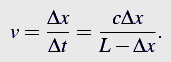
So far, so good. But what has happened to the box’s center of mass? Initially it has been positioned over the point ×c, then the box moved leftwards and stopped. Did the center of mass move as well? Of course, not. There was no external force acting on the system, so the center of mass remained at the initial position.
Summarizing, there are two undeniable facts
1. The box moved,
2. Its center of mass did not.
The only way out of the apparent contradiction is to admit, that besides the energy and momentum the photon carried some mass m from the left to the right wall. (Notice, thatm is not the rest mass of the photon. Photons have zero rest mass.)
From the momentum conservation, the magnitudes of momenta of the box and photon are equal
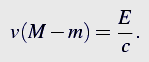
Substituting the previously evaluated velocity v in the expression above one gets
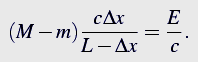
For the center of mass to remain still, the mass displacement of the box must be balanced by displacement of the mass carried by the photon.
![]()
From the two last equations one obtains
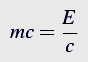
Or in more recognizable form:
![]()
Sanity check: Has any Special Relativity been used in this derivation?
The original idea, similar to the box example, comes from A. Einstein (1906).
¹ The dispersion relation for light is derived from Maxwell’s equations in vacuum. First convert them to a wave equation for the magnetic field B and then try a solution B=B0cos(kx-wt).
Zbigniew Karkuszewski, March 14-th 2008