Ten, kto zastanawiał się jak wyprowadzić wzór E=mc² to pewnie wie, że sprawa nie jest prosta. Na przykład wydaje się, że do tego potrzebna jest znajomość Szczególnej Teorii Względności albo nawet, Boże uchowaj, jej zrozumienie.

Otóż nic podobnego! Aby wzór ten wyprowadzić wystarczy rozwiązać elementarną zagadkę.

Na rysunku znajdują się kontury spoczywającego pudła o masie M i środku masy wypadającym gdzieś ponad punktem ×c. Długość poziomego boku oznaczona jest jako L.

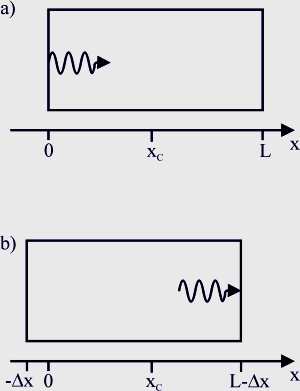
Zagadka jest następująca: Co się stanie z położeniem środka masy pudła jeśli z jego lewej ścianki zostanie wyemitowany foton, który później będzie pochłonięty przez prawą ściankę?

Przyjmijmy, że foton miał energię E. Wiadomo¹, że foton porusza się z prędkością światła c i ma pęd

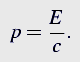
Z zasady zachowania pędu wynika, że pudło po emisji fotonu musi poruszać się w lewo z pewną prędkością v. Po wchłonięciu fotonu przez prawą ściankę pudło zatrzyma się zgodnie z zasadą zachowania pędu.

Prędkość v można wyliczyć tak. Zanim foton uderzy w prawą ściankę pudło przesunie się na odległość Δx w lewo. Czas Δt w jakim to przesunięcie nastąpiło jest dany przez czas w jakim foton pokonał odległość L-Δx czyli

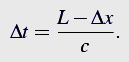
Zatem średnia prędkość pudła v wynosi

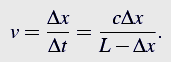
No dobrze ale co się stało ze środkiem masy pudła? Na początku był on nad punktem ×c, później pudło przesunęło się w lewo i znieruchomiało. Czy środek masy przesunął się razem z pudłem? Oczywiście nie, na pudło nie działała żadna zewnętrzna siła. Środek masy nie miał prawa się przesunąć!

Mamy więc dwa zdumiewające fakty:
1. Pudło przesunęło się w lewo,
2. Jego środek ciężkości pozostał w miejscu.

Te dwa fakty mogą być pogodzone tylko wtedy jeśli razem z fotonem z lewej ścianki na prawą przeniosła się część masy pudła. Oznacza to, że fotonowi oprócz energii i pędu można przypisać jeszcze masę m. (Uwaga: nie jest to masa spoczynkowa fotonu. Fotony mają zerową masę spoczynkową.)

Z zasady zachowania pędu wynika równość pędu pudła i fotonu

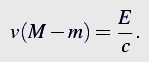
Do tego wyrażenia wstawiamy wyliczoną wcześniej prędkość

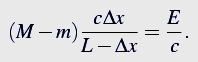
Aby środek masy całego układu pozostał w miejscu to przesunięcie masy pudła musi być zrównoważone przemieszczeniem masy fotonu, zatem

Kombinując dwa ostatnie równania dostajemy

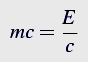
czyli

Dla dociekliwych: Czy do wyprowadzenia tego równania potrzebna była mechanika relatywistyczna?

Oryginalny pomysł pochodzi od A. Einstein’a (1906).

¹ Relacja dyspersji dla światła pochodzi z rozwiązania równań Maxwell’a w próżni. Wyprowadzenie polega na sprowadzeniu tych równań do postaci równania falowego na B i wstawieniu weń rozwiązania B=B₀cos(kx-wt).

Zbigniew Karkuszewski, 14 marca 2008